
Doris, a glassknife fish
Overview and Motivation
My interest in studying unique locomotion motivated me to join the Locmotion in Mechanical and Biological Systems Lab where I studied methods to track the ribbon-fin of a glassknife fish using Deep Lab Cut(DLC).
The objective of the project is to to track the motion of the undulatory ribbon-fin of a glassknife fish, Eigenmannia virescen effectively.
This fish’s swimming motions are unique and interesting from a locomotion perspective because of the complex mechanics of the two counter propagating waves produced by the fish, one starting from the head and the other starting from the tail.
These waves help the fish swim forward and backwards without moving it’s body too much.
Tracking of the fin is a challenging problem because the number of waves produced at each time step might vary and tracking a point on the wave is not equivalent to tracking a point on the fin. This idea, a lot of trial and test, and co-ordinate frame transformations were used to track the fin efficiently.
- Languages: MATLAB
- Framework: Deep Lab Cut (DLC)
- Skills : Locomotion Dynamics, Principal Component Analysis, State Estimation
Approach
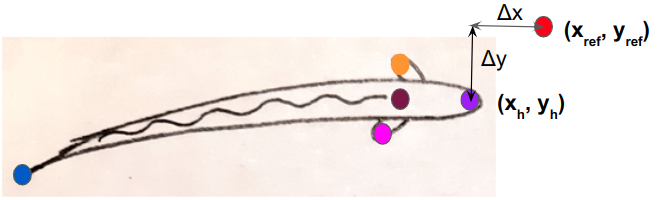
Head and Body Center Orientation
Two stationary points that are easy to track are bodycenter and the head. Along with the head, the body center, the pectoral fins,
the tail and a point on the shuttle was tracked. The fish naturally follows the shuttle and tries to stay inside the
shuttle. But even for stationary shuttle experiments, the position of the head changes with each frame. Having
the same coordinates for the head position in all frames is useful in efficient tracking. Frames were extracted from
the analysed DLC video. The head position of the first frame was used as the reference position. Head positions
from all other frames were moved to this point as described in the following equations:
\[\begin{matrix}
\Delta x & = & x_{ref} - x \\
\Delta y & = & y_{ref} - y \\
x_{h_{new}} & = & x_h + \Delta x \\
y_{h_{new}} & = & y_h + \Delta y \\
\end{matrix}\]
| Frame translation |
Frame rotation |
 |
 |
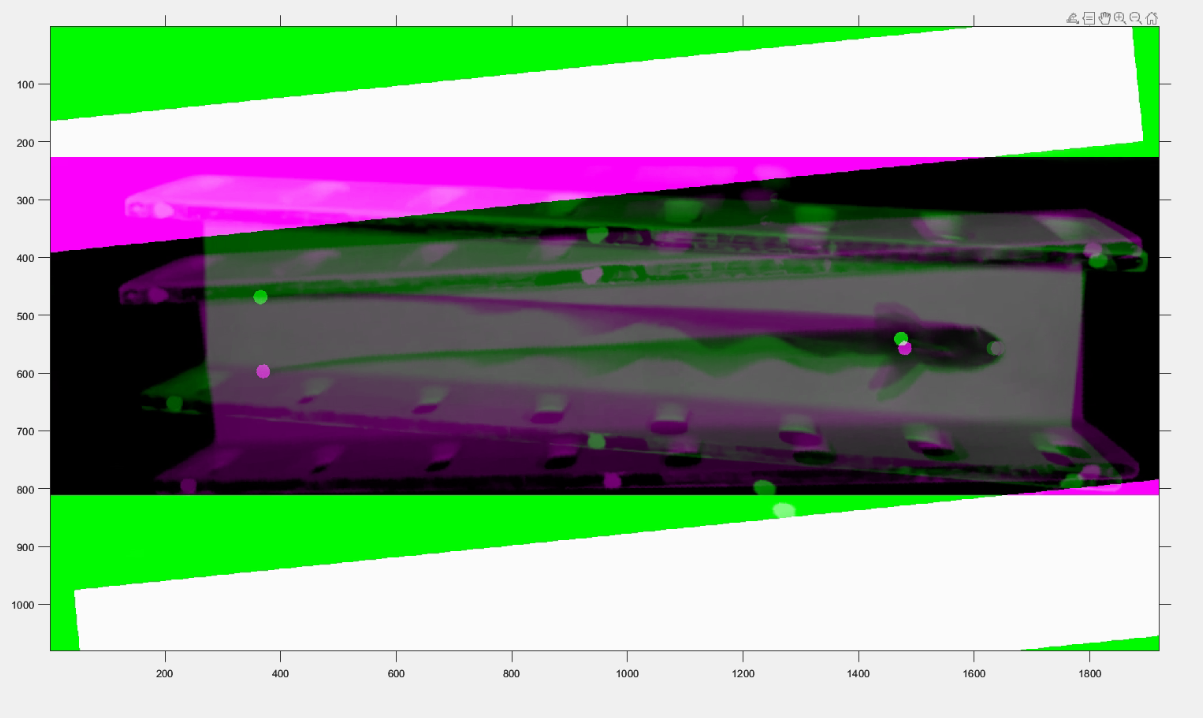
Another important aspect is to orient the body center on the same line as the head. This implies that the
x-coordinates of the body center and head might be different but the y-coordinates have to be very similar. This
translation and rotation can be done using co-ordinate frame transformations. The frame is translated to move
the head position to the reference point and then frame is rotated in clockwise direction if the angle between the
head and the body center is positive and in anticlockwise direction if this angle is negative.
\[\begin{matrix}
\Delta \theta & = & tan^{-1}(\frac{y_h - y_b}{x_h - x_b}) \\
l & = & \sqrt{(x_{h_{new}} - x_{b_{new}})^{2}+(y_{h_{new}} - y_{b_{new}})^{2}} \\
(x_{b_{new}}, y_{b_{new}}) & = & (x_{b_{new}},y_{b_{new}} \pm l \Delta \theta) \\
\end{matrix}\]
| Overlap check after rotating the initial frame |
Overlap check after the transformation |
 |
 |
Line generation for tracking
DLC collects the pixel coordinates marked during labeling. These coordinates are used to train the network. And
hence it is crucial to feed and label the right data to obtain accurate results. Lines were earlier used to track the fin points.
But my contribution was to implement having all the lines in every frame to label all points at once. Starting from a fixed distance from the head position, 56 lines were drawn perpendicular to the line joining the head and the body center. This was to avoid errors in labeling and to make sure that points are being tracked accurately.
For the videos chosen, 56 lines covered all of the fin and the body of the fish. It is
important to note that fixing the head at the reference position will help in drawing the lines at fixed distances
from this position. The fin line of the fish was also tracked to interpolate the data correctly for data analysis.
The same strategy for labeling and training was also used to track almost 56 points on the body-line.
DLC details
- DeepLabCut version 2.2.3 was for this project
- Videos with 56 lines on each frame was used for fin tracking
- 150 frames were extracted for labeling each video using kmeans clustering algorithm inbuilt in DLC
- The cluster step chosen was 1
- Resnet 50 network was used to train the labeled dataset and the augmentation method used was imgaug
- Maximum iterations were set to 25,000
Result
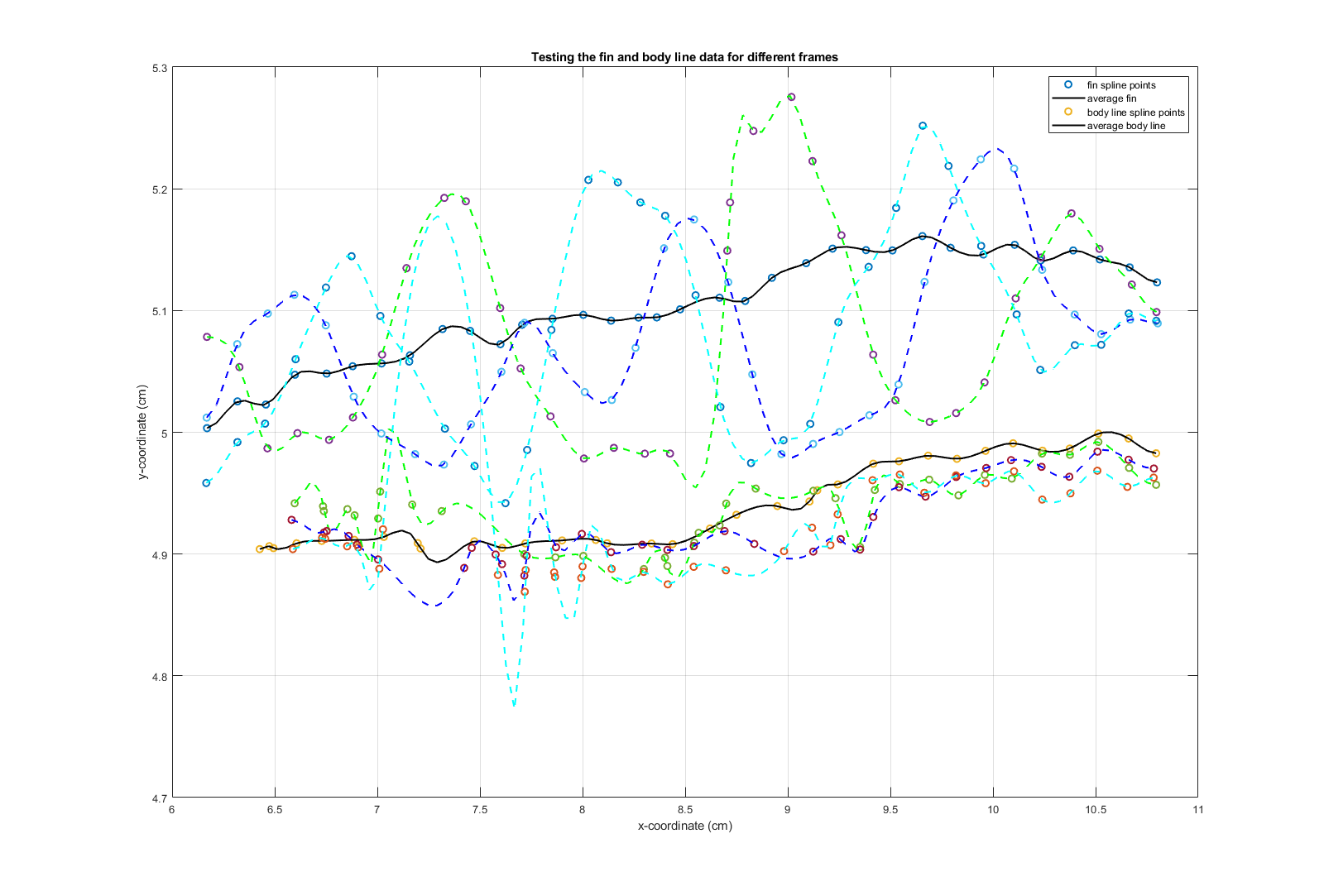
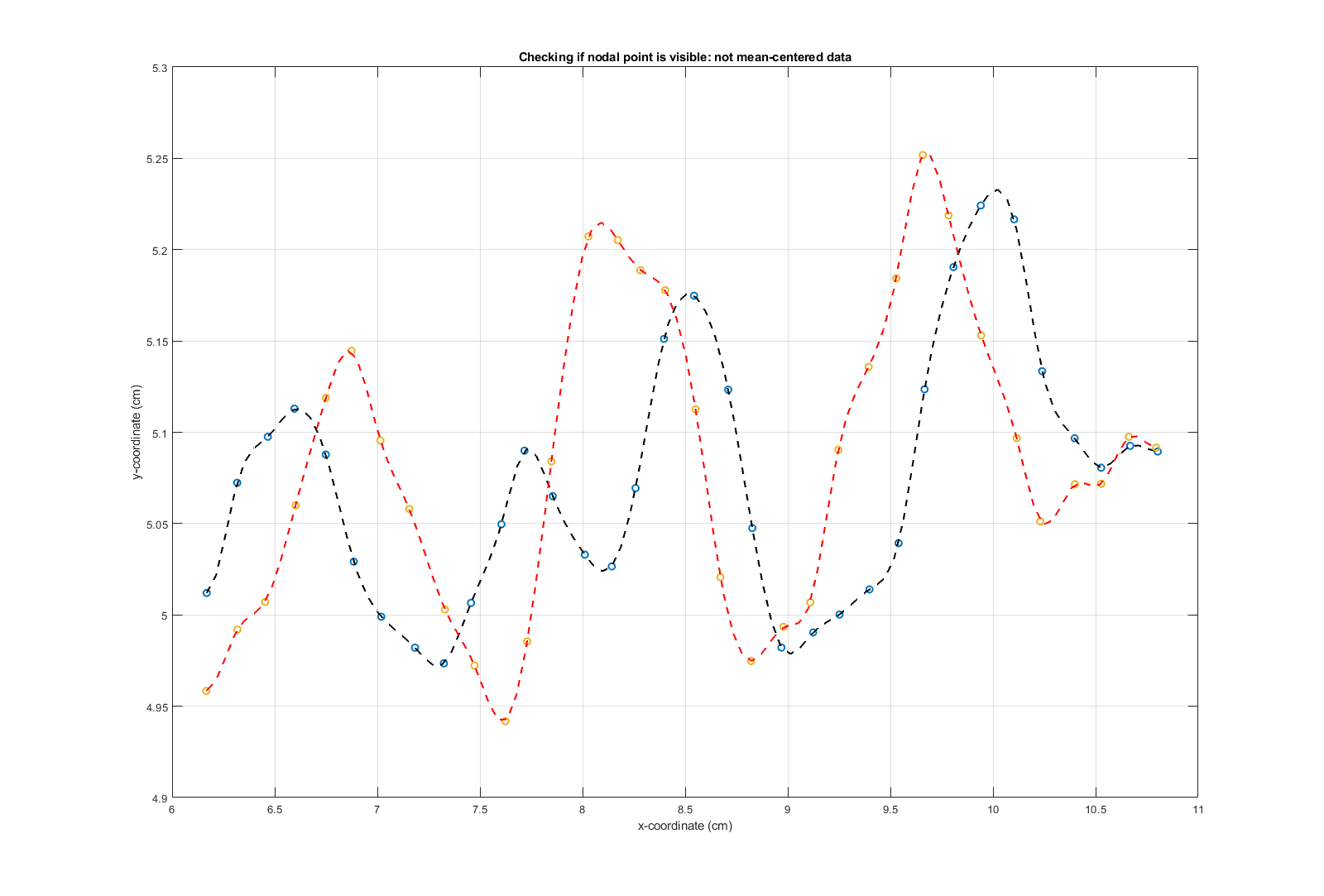
The points on the fin and the body line were tracked with more than 95% accuracy on an average. However, it is evident to see the dynamically moving nodal point where the
waves cancel out. DLC could not track this point accurately since it was not predictable.
The datasets from the tracking algorithms were used to find wave parameters such as wavelength, frequency,
time period and amplitude. A conversion factor was found based on the length of the actual fish in cm and the
length in pixels from the data. This conversion factor was used to plot and analyse the data in cm. Used curve fitting tools in MATLAB to fit the bodyline and fin data. PCA raw data was obtained by considering x-coordinates of the fin data
as the rows and each column as a complete fin. Each columns represent the fin at a given frame.
| Testing the fin and bodyline data for selected frames |
Checking the visibility of nodal point |
 |
 |
Challenges
- The fish is 6.5-7 cm long on an average. It was very challenging to capture clear videos of the transparent fin
- Changing head and body center position for all frames
- Feeding the right data to DLC - solved with the line generation approach