Overview and Motivation
The study was motivated by symmetries in gaits. A mathematical understanding of gaits has been established. Gait maps were studied based on the position of the legs and the ground contact at any given time. Different possible permutations for a given gait were obtained from the map study of a gait. This was later used to understand the symmetries in permutations and the composition of these initial permutations. The permutations and their compositions were then classified based on the group-theory framework.
- Languages: MATLAB
- Skills : Central Pattern Generators, Nonlinear modeling, Gait Analysis
Approach
Gaits are a series of limb motions that are cyclic or
symmetric in nature. Gaits occur during animal locomotion. Different quadruped gaits like horse’s canter, trot, traverse gallaop, camel’s pace and rabbit’s bound were studied based on gait maps provided in the famous paper Coupled nonlinear oscillators and the symmetries
of animal gaits by J.J.Collins. Spatial, temporal and diagonal symmetries in these gaits were studied using groups and lie algebra.
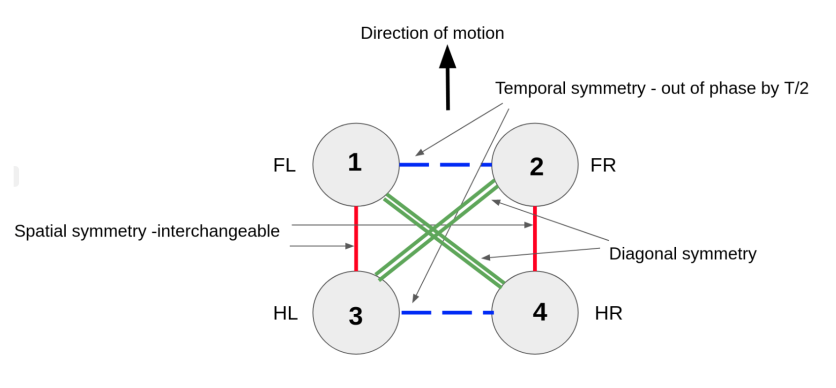
A Kuramoto nonlinear oscillatory model was developed to play with various permutations of these gaits to verify stability using phase trajectories. The states of the legs give the phase of the gait. The states of the system are \([\theta_{1}(t),\ \theta_{2}(t),\ \theta_{3}(t),\ \theta_{4}(t)]^{T}\), where \(\theta_{1}(t)\), \(\theta_{2}(t)\), \(\theta_{3}(t)\), and \(\theta_{4}(t)\) are the states of the fore left, fore right, hind left and hind right legs. In case of a quadruped, each leg is
represented as an oscillator. A quadruped is an ODE system of four equations. The model accounts for the coupling and decoupling between the legs. The oscillators were coupled based on the symmetry in a given gait. The model used was:
\(\dot{\theta_{k}}(t)\ =\ \omega_{k}(t)\ +\ \sum_{j=1}^{n}c_{k,j}sin(\theta_{j}-\theta_{k})\ ;\ k\ =\ 1,2,3,4\)
Composition of different permutations were done after the oscillators were coupled. This should still retain the coupling between the oscillators and this behaviour was observed.
Result
| Phase trajectories of a 4 oscillator nonlinear dynamic model |
Rotary Gallop of a cheetah |
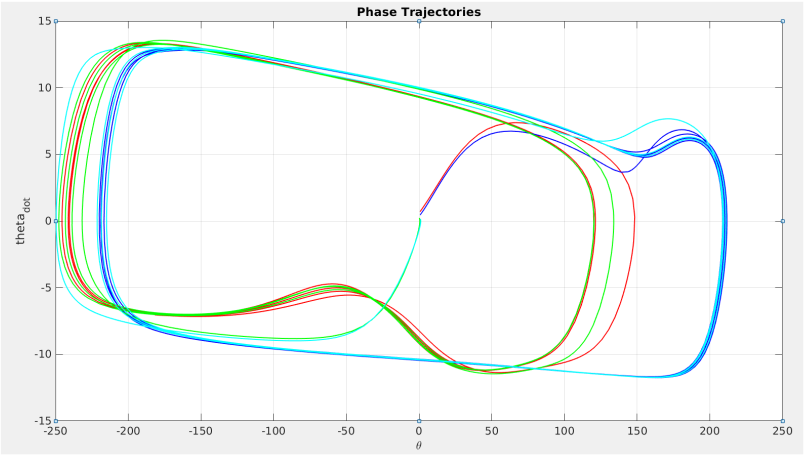 |
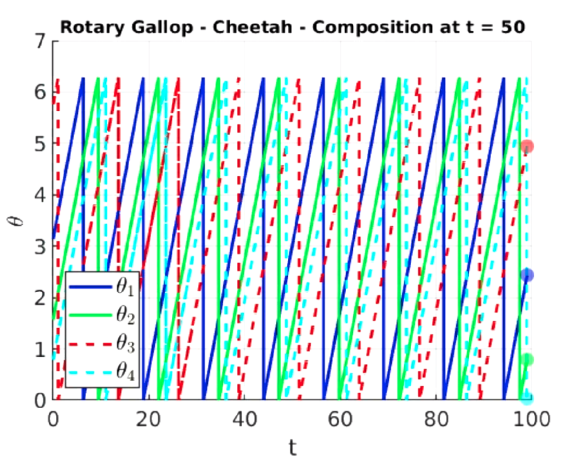 |
Challenges
- Understanding the coupling and decoupling sequences in an animal gait and establishing a mathematical relationship for these symmetries is a challenging task.
- The framework does not address nonsymetry in gaits. However stability analysis of the gaits in the presence of a non-
functioning leg or a limping leg can be an extension to this project.